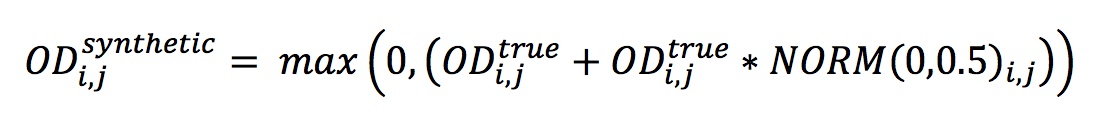1. Introdução

O ajuste de matriz é um procedimento para ajustar uma matriz OD, a priori, usando contagens de tráfego de detectores, estações de detectores, seções viárias ou movimentos de nós ou supernós. O algoritmo de solução é baseado em um modelo de dois níveis, resolvido heuristicamente por um algoritmo de gradiente e inclui uma alocação em cada iteração. O algoritmo pode ser visualizado como o cálculo de uma seqüência de matrizes OD que reduzem consecutivamente o erro de mínimos quadrados entre as contagens de tráfego provenientes dos detectores e os fluxos de tráfego obtidos por uma alocação de tráfego.

O algoritmo usado para resolver o problema é de natureza heurística, do tipo de descida mais íngreme, e não garante que um ótimo global para o problema formulado seja encontrado. Portanto, às vezes, a intervenção manual é necessária para obter um bom resultado.

O Aimsun Next fornece várias opções para limitar o processo de ajuste para evitar overfitting e permanecer tão próximo quanto da matriz original. Por exemplo, a elasticidade da matriz e a elasticidade da distribuição do comprimento da viagem podem ser configuradas para definir globalmente um limite de mudança da matriz original. Em alguns casos, uma matriz de desvio máximo pode ser fornecida para definir com precisão um limite de mudança para cada par OD individual. A função de peso pode ser usada para atribuir pesos diferentes aos valores observados (dados reais) que são usados ​​para o ajuste.

O uso da função de peso é o menos explorado dessas opções. A função de peso é a única opção que influencia diretamente os valores observados e, além disso, uma questão conhecida de erros mínimos quadrados é que ela favorece os valores altos. A função de peso, se usada adequadamente, poderia reduzir o desequilíbrio entre as contagens altas e baixas e, assim, melhorar o resultado geral do ajuste.

Esta nota técnica explora o impacto da função de peso no processo de ajuste da matriz.

2. Modelo de testes e dados

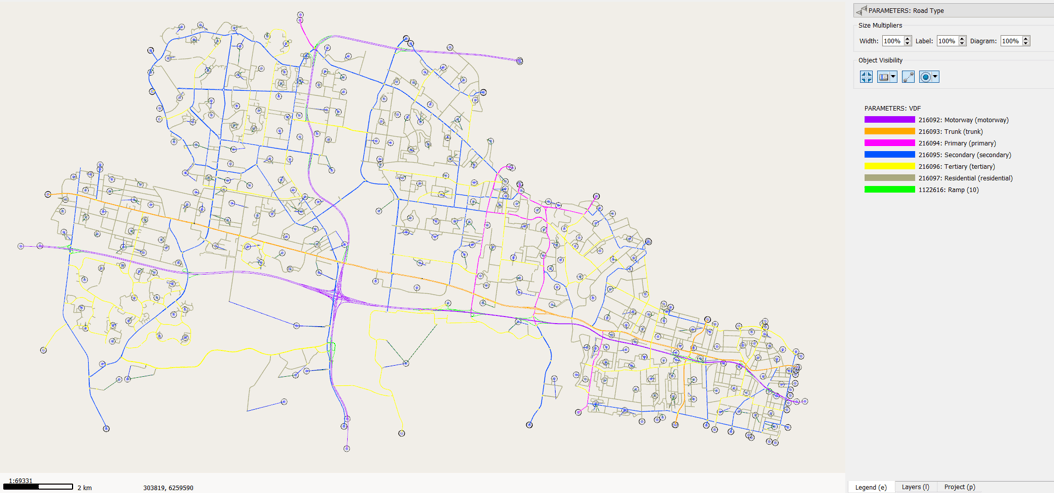
A demanda de base para o ajuste de OD é derivada do modelo estratégico no Emme. Os dados dos detectores utilizados neste estudo são combinados a partir de duas fontes diferentes: os dados da rodovia foram recolhidos dos detectores de rodovia que registram contagens individuais de veículos a cada 3 minutos. A maior parte das interseções semaforizadas tem contagens de interseções coletadas do banco de dados histórico do SCATS. Os dados do SCATS são armazenados em intervalos de 1 a 5 minutos. O conjunto de dados combinado foi ajustado para intervalos de 15 minutos. Estes dados do detector são posteriormente combinados com os dados da estação do detector (uma estação detectora em uma seção de estrada é uma coleção de detectores com uma direção comum de viagem).

O modelo abrange estradas locais à vias expressas e tem um total de 1.236 estações de detectores, das quais 203 estão em auto-estradas e o resto em interseções urbanas semaforizadas. A extensão do fluxo observado em diferentes detectores varia de 0 a 6.070 veíc / h.

Figura 1: Mapa da rede mostrando os tipos de vias

3. Impacto da função de peso no ajuste da matriz

3.1 Função de peso

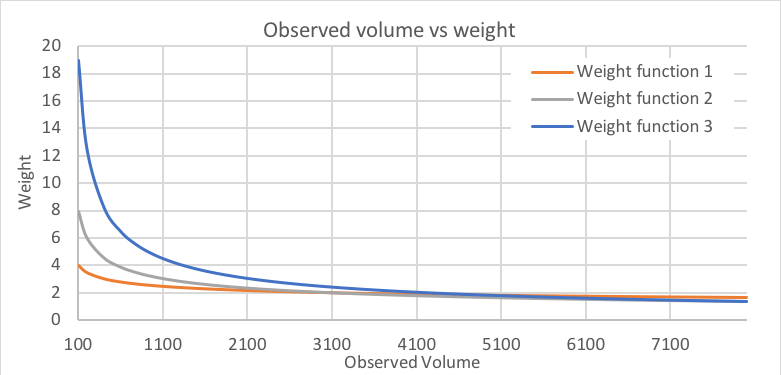
Uma função de peso de ajuste pode ser usada como uma forma de confiabilidade dos dados reais (seção / detector / contagem de movimentos) usada para o processo de ajuste. Por padrão, nenhuma função de peso é aplicada. As seguintes funções de peso foram aplicadas neste estudo:
Função de peso 1 = (1 / (Volume observado ^ 0,2)) * 10
Função de peso 2 = (1 / (Volume observado ^ 0,4)) * 50
Função de peso 3 = (1 / (volume observado ^ 0,6)) * 300

Figura 2: Peso vs volume observado

3.2 Impacto da função de peso no desempenho do ajuste de OD

Para entender o efeito da função de peso no ajuste da matriz, quatro diferentes ajustes estáticos foram realizados: usando nenhuma função de peso, e usando a função de peso 1, 2, 3. Os experimentos de ajuste estático tiveram as seguintes configurações:

• Número de iterações externas = 20 • Número de iteração descendente de gradiente = 3 • Número de iterações internas = 50 • Diferença relativa = 0,1% • Método de atribuição = Frank e Wolfe Conjugado

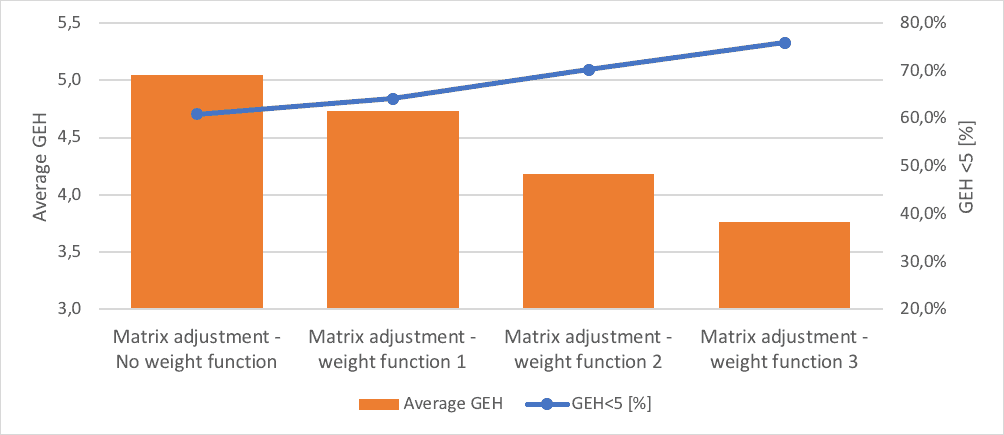
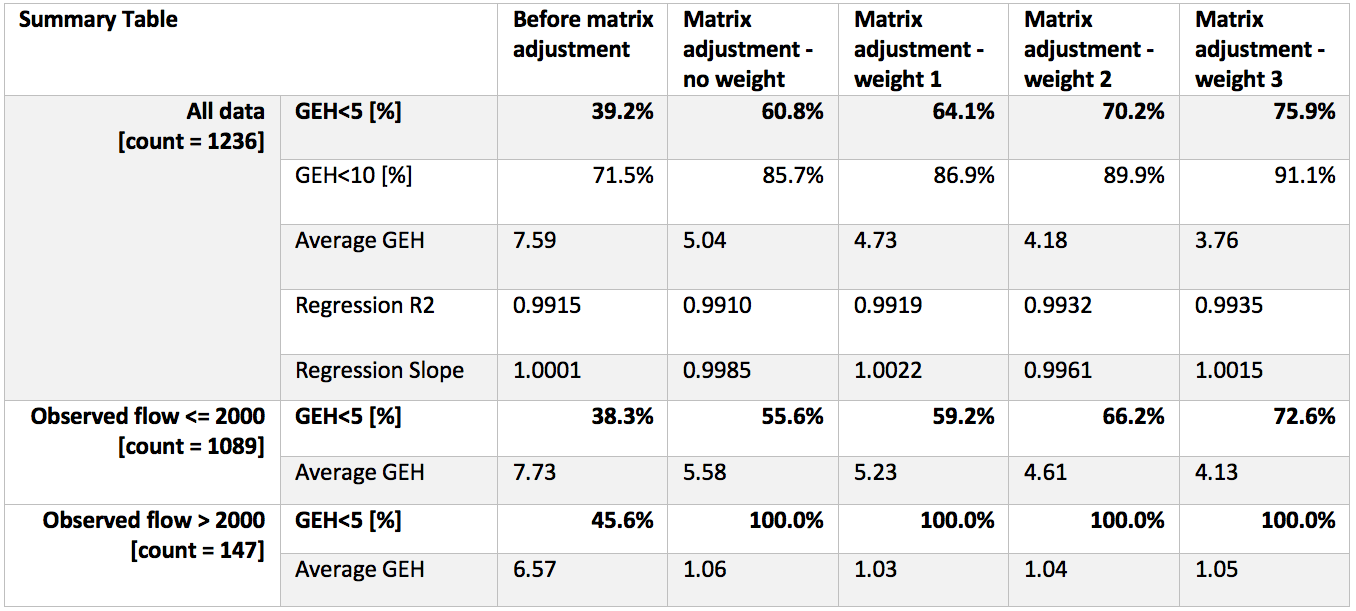
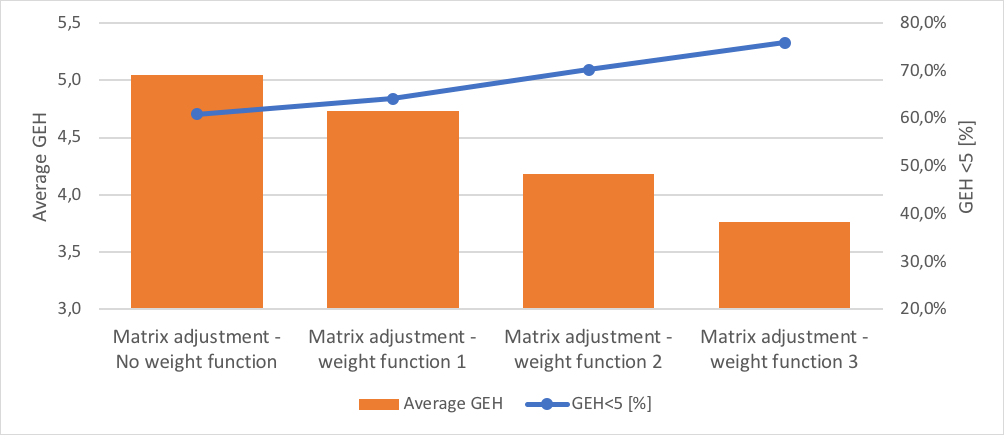
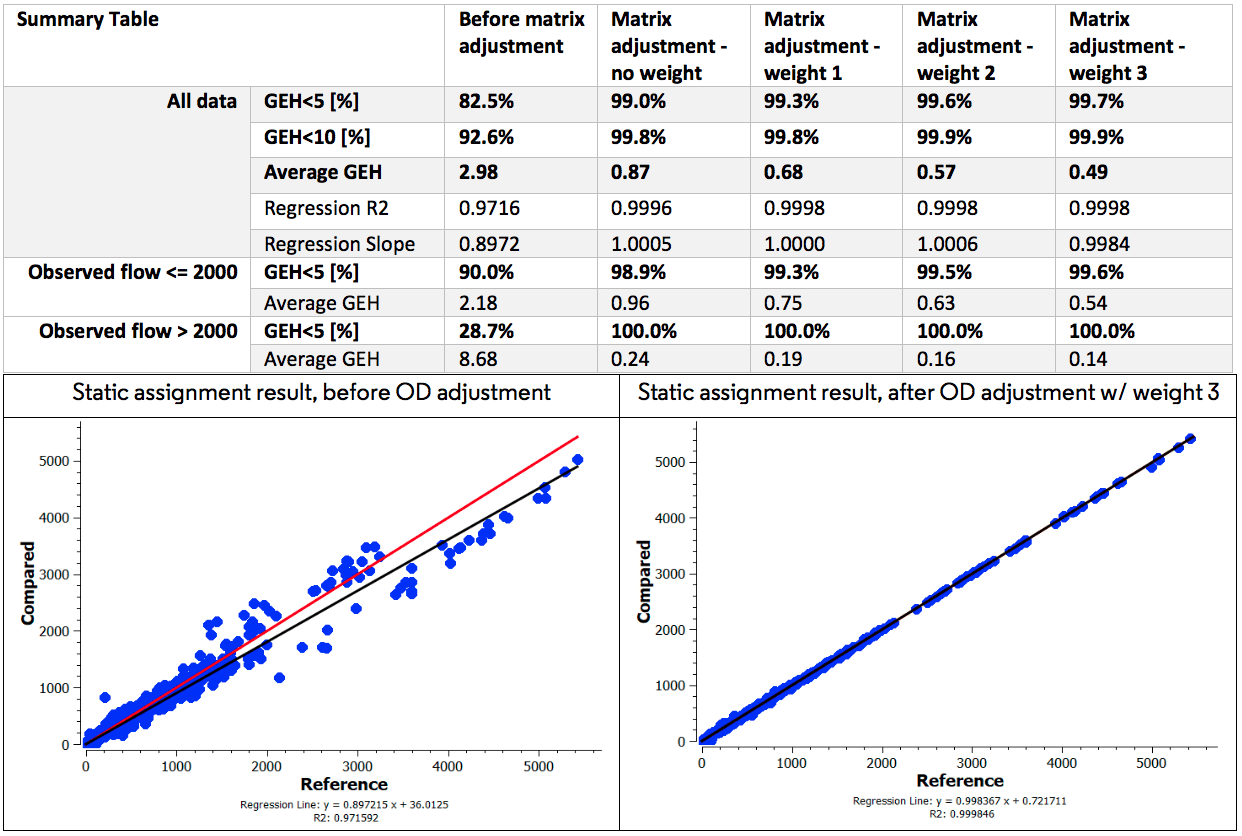
A Tabela 1 apresenta o resultado dos experimentos de ajuste de matriz. O desempenho do ajuste é validado com o fluxo observado e simulado. Os principais critérios para validação são GEH <5%, nível médio de GEH e regressão R2.

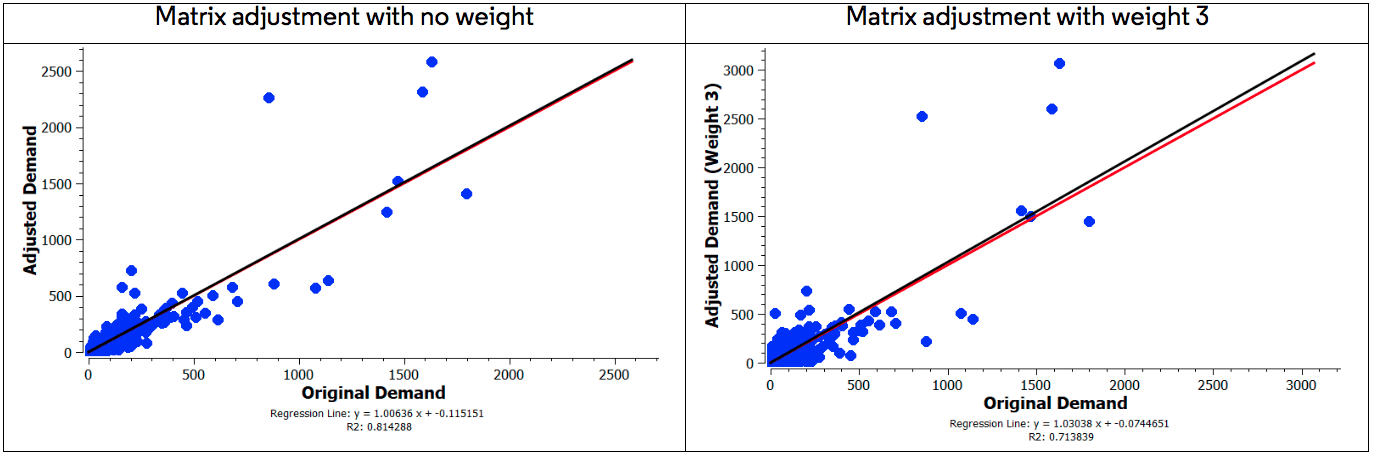
A Tabela 1 mostra que, mesmo sem usar qualquer função de peso, o ajuste da matriz faz um bom trabalho. O GEH <5% para todos os dados é de cerca de 61%, enquanto para o fluxo observado acima de 2000 é de 100%. Uma questão conhecida do ajuste de matriz é que ela favorece o fluxo alto, pois o algoritmo usa o erro de mínimos quadrados entre as contagens de tráfego provenientes dos detectores e os fluxos de tráfego obtidos por uma atribuição de tráfego. Portanto, quando usamos uma função de peso que dá alto peso a contagens pequenas, é provável que melhore o desempenho do ajuste. A Tabela 1 mostra que, usando o peso 3, o GEH global <5% melhorou para 76%. A função de peso reduziu o nível médio de GEH.

Curiosamente, o GEH médio para o fluxo observado acima de 2000 aumentou com o aumento do peso, enquanto o oposto é observado para o fluxo abaixo de 2000. Esse comportamento é causado pela natureza da função de peso utilizada neste estudo, que coloca mais peso sobre o pequeno fluxos. Assim, a matriz ajustada mostrou melhor desempenho para as estradas locais, ou seja, estradas com vazão <2000 veh / hr.

Tabela 1: Impacto da função peso no desempenho do ajuste da matriz

Figura 3: Impacto da função peso no desempenho do ajuste da matrizA aplicação da função de peso melhora claramente o desempenho de ajuste. No entanto, a função peso pode criar mais distorção na matriz original em comparação com o ajuste sem função de peso. Por exemplo, a figura a seguir indica a quantidade de distorção da matriz através do gráfico de dispersão da demanda ajustada versus demanda original. O valor da regressão R2 para sem peso e peso 3 é de 0,8143 e 0,7138, respectivamente. O uso do peso 3 criou mais distorção para a matriz original para melhor corresponder ao fluxo observado.

Dependendo do tipo de função de peso, a distribuição do comprimento da viagem pode variar. Por exemplo, neste estudo, a função de peso favorece pequenos fluxos que podem aparecer nas estradas locais. Portanto, uma função de peso alto criará mais viagens de curta duração do que nenhuma função de peso (veja a figura a seguir).

A partir da discussão acima, fica claro que a função de peso é uma ferramenta poderosa para o ajuste de matriz. No entanto, os usuários devem ter cuidado ao superequipar o modelo. Um equilíbrio entre as áreas de fluxo baixo e alto da rede deve ser mantido selecionando uma função de peso apropriada.

Figura 4: Impacto da função peso na deformação da matriz e na distribuição do comprimento da viagem

3.3 Impacto da iteração descendente de gradiente no desempenho do ajuste de OD

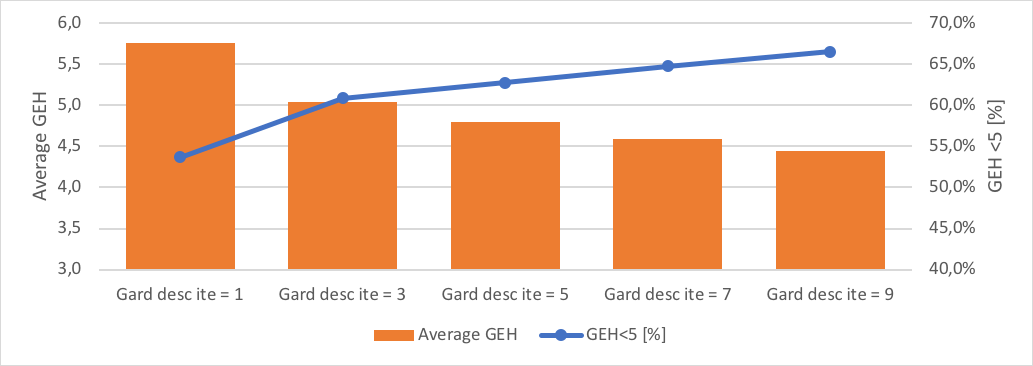
Na estrutura de otimização de dois níveis para ajuste de matriz em Aimsun Next, o método de descendente de gradiente é executado sem alterar os resultados de escolha de caminho obtidos da alocação estática que foi executada na iteração externa. Uma iteração descendente de gradiente mais alta deve melhorar o ajuste da matriz com o custo de maior tempo de execução. No teste anterior, usamos iteração descendente de gradiente = 3. Nesta seção, observaremos o impacto da iteração descendente de gradiente no desempenho de ajuste da matriz sem peso como o caso base. A Tabela 2 apresenta o efeito da iteração descendente de gradiente no desempenho do ajuste da matriz. Nenhuma função de peso foi usada.

Tabela 2: Impacto da iteração descendente de gradiente no desempenho do ajuste de matriz

Figura 5: Impacto da iteração descendente de gradiente no desempenho do ajuste de matrizUma observação atenta das mudanças na média GEH ou GEH <5% mostra uma mudança rápida no desempenho do ajuste da matriz entre as iterações número 1 e 3. As mudanças no desempenho do ajuste da iteração descendente de gradiente 3 a 9 são quase lineares. Portanto, no restante da análise, uma iteração descendente de gradiente = 3 foi usada.

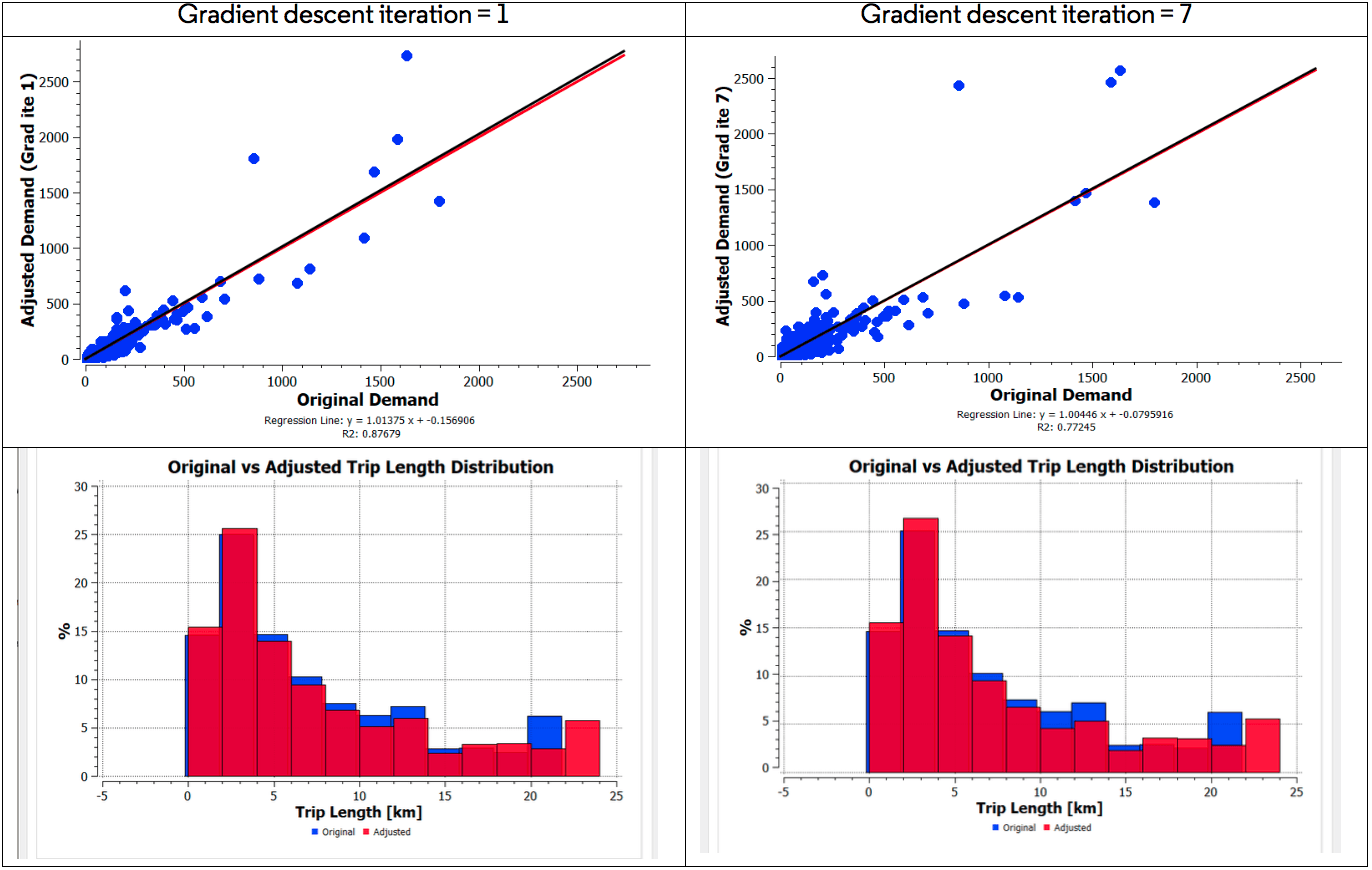
A melhoria no ajuste da matriz vem com maior deformação da demanda original e distribuição do comprimento da viagem. Na Figura 6, uma comparação entre a deformação da matriz e a distribuição do comprimento da viagem é mostrada entre a iteração descendente de gradiente 1 e 7. A regressão R2 foi reduzida para 0,77 com 7 iterações de descida em comparação com um valor de R2 de 0,88 com apenas 1 iteração de descida. Da mesma forma, um número maior de viagens curtas é observado com o aumento da iteração descendente de gradiente.

Figura 6: Impacto da iteração descendente de gradiente na deformação da matriz e distribuição do comprimento de viagem

4. Impacto da função de peso na distorção da matriz

Até agora, a análise foi realizada em dados reais coletados de diferentes fontes. A demanda base vem de um modelo estratégico. Como os dados usados ​​para ajuste vêm de fontes diferentes, é difícil saber qual é o mais confiável. Ao impor um peso diferente ou controlar outros parâmetros, o processo de ajuste produz uma saída que foi distorcida da matriz de entrada (base) para ajustar as contagens. No entanto, não temos ideia de quão próximo o resultado do ajuste é da matriz verdadeira. A matriz verdadeira é uma matriz hipotética que (se disponível) produziria as mesmas contagens do detector.

Nesta seção, realizamos um teste hipotético para observar se a função de peso ajuda a produzir uma matriz de demanda próxima da demanda real. Observamos que a função peso fornece melhor desempenho para ajuste de matriz. No entanto, o melhor desempenho vem com o custo de maior deformação da matriz de entrada e maiores mudanças na distribuição do comprimento da viagem. Seria interessante saber se essas mudanças produziram uma matriz mais próxima da matriz verdadeira. Se o resultado estiver mais próximo da matriz verdadeira, as deformações mais altas na matriz de entrada devem ser aceitáveis.

4.1 Criação de demanda verdadeira e sintética e RDS a partir da demanda real

Tomamos a demanda ajustada da seção 3.2 com a função de peso 3 (como produziu os melhores resultados de ajuste). Nós tomamos essa demanda como a “demanda real”. O fluxo de equilíbrio gerado a partir desta demanda real nas estações de detecção é denominado como o RDS real. Este RDS real é um RDS perfeito, livre de qualquer erro de observação, e todo o fluxo do detector é consistente com os fluxos a montante, a jusante, bem como entre todas as outras abordagens de uma interseção.

A  demanda real foi distorcida pela adição de um ruído branco e denominada “demanda sintética”, que será usada para ajuste de matriz. O ruído branco é produzido a partir de uma distribuição normal com média = 0 e desvio padrão = 0,5, semente = 1. A demanda sintética é criada seguindo esta fórmula:

Onde i e j denotam origem e destino respectivamente.

No mundo real, não temos acesso a essa “demanda real”. Só teremos acesso à ‘demanda sintética’. Assim, este teste fornecerá algumas informações valiosas sobre o quão próximo o ajuste pode aproximar a matriz da demanda original / verdadeira.

4.2 Resultado do ajuste de OD com demanda sintética e RDS real

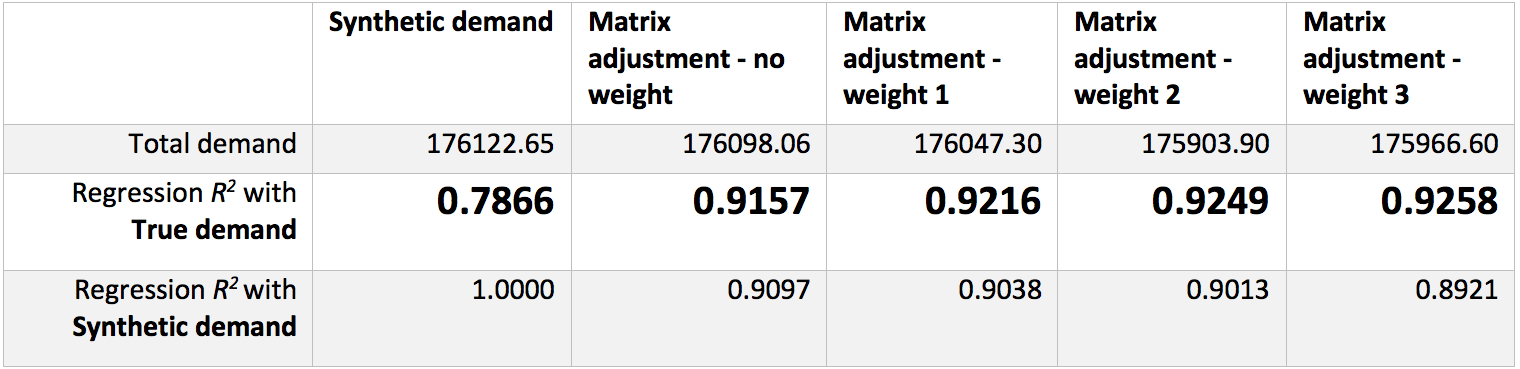
A Tabela 3 apresenta o resultado do ajuste com demanda sintética e RDS real. Como havíamos observado antes, a função de peso fez um bom trabalho. Mesmo sem usar a função de peso, o resultado é bom. O motivo é provavelmente devido à qualidade do RDS. Como o RDS está livre de inconsistência no fluxo, o processo de ajuste teve menos dificuldade em encontrar mínimos globais.

Tabela 3: Impacto da função de peso no ajuste da matriz com matriz sintética e RDS realComo agora temos acesso à matriz verdadeira e sintética, podemos comparar a qualidade da matriz ajustada. A Tabela 4 apresenta os valores da regressão R2 entre a demanda ajustada e a verdadeira. Também mostra os valores da regressão R2 entre a demanda ajustada e sintética.

Tabela 4: impacto da função peso na deformação da matrizA função de peso criou mais deformação para a matriz sintética que foi usada para o ajuste (a regressão R2 entre a demanda sintética e ajustada é a mais baixa para a função peso 3 e a mais alta para o caso sem peso). Curiosamente, o oposto é observado para a demanda real. Essa alta deformação levou a matriz para mais perto da matriz verdadeira. A regressão R2 entre a demanda ajustada e a verdadeira é a mais alta para a função peso 3 e a menor para o caso sem peso. Claramente, a função de peso deformou a matriz na direção certa para criar uma demanda ajustada que represente de perto a demanda real.

5. Resumo

• O uso da função de peso de ajuste pode melhorar significativamente o desempenho do ajuste da matriz.
• Na maior parte do projeto, o objetivo é atingir uma alta porcentagem de GEH <5. O processo de ajuste normal maximiza o valor de R2, no entanto, ele não tem controle sobre o GEH.
• Este estudo encontra uma relação estreita entre a função de peso e o GEH. Aumentar a função de peso ajudou a reduzir o nível médio de GEH e aumenta a porcentagem de GEH <5.
• A função de peso cria uma maior deformação na matriz de base em comparação com o ajuste sem função de peso – também, a distribuição do comprimento de viagem muda até certo ponto.
• Uma iteração descendente de gradiente alto ajuda a melhorar o desempenho do ajuste.
• Recomenda-se uma iteração descendente de gradiente ≥ 3.
• A qualidade do RDS tem um grande impacto no desempenho do ajuste.
• Se pudermos garantir a consistência do RDS, uma função de peso pode levar a matriz ajustada para perto da matriz verdadeira de onde o RDS teria sido derivado.